[CS fundamentals] Red-Black Tree

interview, data structure, cs, red-black, tree · 13 Oct 2020

Red-black tree

red-black tree 란 Binary search tree (BST) 의 일종으로, BST 의 단점 - tree 전체가 balanced 하지 않을 경우 (최악) O(n) 의 시간복잡도를 보임 - 을 개선한 tree structure 입니다.

Example of red-black tree

(참고) 일반적인 BST 는 leaf 에서의 null child 를 별도로 표기하지 않지만, red-black tree 에서는 leaf 를 위한 NIL node 를 사용합니다. red-black tree 에서의 모든 leaf 노드는 NIL 이며, leaf 가 아닌 모든 노드는 2개의 child (NIL or not NIL)를 가집니다.

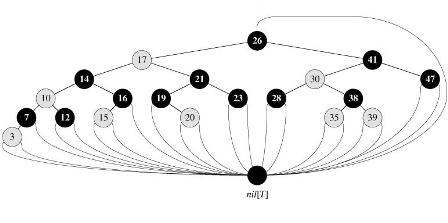
(참고2) Memory 효율성을 위해, 실제 구현시 하나의 NIL 노드 만을 생성하고 모든 leaf 로의 edge 를 여기에 연결시켜 사용하기도 합니다.

Example of single sentinel NIL leaf

핵심적인 특징

BST 의 성질은 그대로 유지 (모든 노드에 대해, 해당 노드의 값은 left child 노드의 값보다 크고, right child 노드의 값보다 작다.)
모든 노드는 RED 혹은 BLACK 의 color 를 갖는다.
모든 최외곽 노드 (root 혹은 leaf) 의 color 는 항상 BLACK 이다. (external rule)
모든 RED 노드의 child 는 BLACK 노드이다. (No double RED, internal rule)
root 노드로부터 leaf 노드까지에 이르는 모든 경로에서 나타나는 BLACK node 의 갯수 (black-height)는 동일하다.

red-black tree 는 삽입, 삭제시 특정 algorithm 을 이용하여 self-rebalancing 을 수행합니다. Recoloring, restructuring (rotating) 의 방법을 이용하여 전체 tree 의 balance 를 유지하며 위 5가지의 특징을 만족하는 상태로 유지하며, balancing 이 완료된 red-black tree 는 root 로부터 leaf 까지의 가장 긴 경로의 길이가 가장 짧은 경로의 길이의 2배 보다 작도록 유지됩니다. (root 노드와 leaf 노드는 항상 BLACK 노드이고, ‘No double RED’ rule 에 의하여 가장 긴 경로는 BLACK(root)-RED-BLACK-…-RED-BLACK(leaf) 의 모양으로 나타나며, 가장 짧은 경로는 경로상의 모든 노드가 BLACK 인 경우이므로 최대 길이 경로의 길이는 최소 길이 경로의 길이의 2배 보다 항상 작다.) 이러한 loosely balanced 상태를 유지하여 search 에서의 시간복잡도를 O(log n) 으로 유지하는 것이 red-black tree 의 핵심 개념이며, 실제로 Java 에서도 Hashmap 의 collision 을 해결하기 위한 하위 자료구조로 red-black tree 를 사용하는 등, 실제 구현에서 상당히 널리 쓰이고 있습니다.

단점 아닌 단점이라면, 삽입insertion 과 삭제removal 시의 algorithm 이 case by case 로 약간은 복잡한 과정을 거친다는 점. 한 번에 이해하기 쉽지는 않지만, 삽입/삭제시 rebalancing 하는 과정을 이해해 둔다면 많은 도움이 될 것입니다.